The Monty Hall problem is a classic probability puzzle based on a game show called Let’s Make a Deal. The problem is named after the show’s host, Monty Hall.
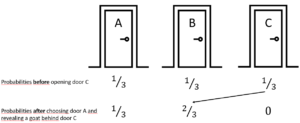
The Monty Hall problem refers to a statistical puzzle that can seem very counter-intuitive. Imagine you participate in a television show, and you are given the choice between three doors (A, B, and C). The host tells you that you will win whatever is behind the door of your choice. He also tells you that behind one of the doors is a new car, and behind the other two doors is a goat. Suppose you choose door A. Then the host (who knows what is behind each door) reveals that behind door C is a goat. You are then given the opportunity to switch to door B, or stick with your original choice. The question is: would that be a smart thing to do? That’s the Monty Hall problem.
Most people think that it does not matter: there is a 1/2 chance the car is behind door A, and a 1/2 chance that the car is behind door B. Most people are wrong… It actually does matter! The probability that the car is behind door B is actually 2/3, so it would be wise to switch. Confused? Let’s look at the math.
The solution to the Monty Hall problem
Why is it better to switch? Suppose I choose door A. There’s a 1/3 chance that this is the door with the car, so there’s a 2/3 chance that the car is behind door B or C. Then the host reveals that there’s a goat behind door C. Remember that the host knows what is behind each door, so he deliberately opens the one with the goat (or picks randomly if both of them have a goat). This revelation gives you new information (the car is not behind door C), so the probability of 2/3 that the car was behind door B or C is now transferred to door B only. The probability that you were right the first time stays 1/3, so you will double your chances if you switch to door B.
A more extreme example
Still confused? Then let’s look at a more extreme example. Suppose that in this version of the game, you have to choose 1 out of 100 doors. You pick door number 21, after which the host opens all the other doors to reveal goats, except door number 87. Would you switch in this case? Your intuition probably tells you that you should switch, which is indeed the right move.
When you choose door number 21, the probability that the car is behind that door equals 1/100. At this point, this probability is the same for all doors in the game. That means that the probability that the car behind one of the other doors is 99/100. Then the host opens 98 other doors to show there is no car behind them. Remember, the host knows where the car is, so he deliberately picks the ones that have a goat. As a result, the probability that the car is behind door 87 changes from 1/100 to 99/100, because all the other doors have been excluded.
The Monty Hall problem and Bayes Theorem
The Monty Hall problem can also be explained using Bayes Theorem. This theorem describes probabilities of an event, given another event occurs. In other words, it uses prior information (probability of a door hiding a car) and the likelihood of observed data (i.e. the probability that the host opens a particular door given the choice and the ). For a full explanation, see this webpage.
Conclusion
The Monty Hall problem is a classic probability puzzle. The solution may seem counterintuitive because it goes against our initial intuition. However, it is mathematically sound and has been demonstrated through various simulations and experiments.